Sommaire

 

 

 

 

LE TRESSAILLAGE article de Smart.Conseil

 

 

               

                  

                     tressaillage,
                     dilatation, dilatomètre, analyse, mesure,
                     instruments de mesure, dilatation thermique,
                     dilatométrie, four, chaleur
                     
                     
 
                  
               
            
            
            
            
            
            
            
            
            
            

 

 

 

 

Présentation du sujet :

 

Les fissures qui apparaissent dans la couche de glaçure dès la sortie du four ou quelques jours plus tard sont du plus mauvais effet lorsqu'elles ne sont pas souhaitées. Contrairement aux idées reçues, ce défaut a plusieurs origines et ne réside pas seulement dans les valeurs du coefficient de dilatation des matériaux en contact. La réalité est plus complexe. L'exposé qui suit montre les principaux facteurs à prendre en compte lorsqu'on veut comprendre et éviter le tressaillage.

 

Le tressaillage est la rupture de la couche de glaçure sous l'effet de contraintes mécanique trop importantes avec le tesson. Il forme un réseau de fissures dont les mailles sont plus ou moins serrées selon l'amplitude des contraintes appliquées, l'épaisseur de la couche de glaçure et ses qualités mécaniques.

 

Le mot " trésaillage " est aussi utilisé pour désigner le tressaillage (" Crazing " in english)

 

Principaux facteurs du tressaillage :

 

- Coefficients de dilatation glaçure / tesson

- Couche intermédiaire

- Élasticité de la glaçure

 

 

I ) Coefficients de dilatation :

 

Règle universelle : Le coefficient de dilatation de la glaçure doit toujours être inférieur à celui de la pâte.

 

Ce coefficient s'exprime en m/m °C, mètre par mètre par degré, soit des °C-1 si on simplifie l'écriture. Ce coefficient est donné par le dilatomètre, appareil qui mesure l'allongement d'un barreau de pâte ou de glaçure en fonction de la température.

La valeur mesurée est très faible tant pour les pâtes que pour les glaçures. Une glaçure ou une pâte s'allongent d'environ 2,5 à 4,5 mm par mètre si on les échauffe de 500°C.

Si on ramène cet allongement par degré, ces valeurs vont de 50 x 10-7 °C-1 à 90 x 10-7 °C^-1. L'allongement d'un barreau de 1 mètre de glaçure ou de pâte varie donc entre 5 et 6 millionièmes de mètre (microns) par degré… c'est peu, mais en céramique ces valeurs sont déterminantes. A température ambiante ces matériaux sont peu déformables et les contraintes qu'ils subissent doivent être contenues en dessous des limites de rupture pour éviter tout dommage.

 

Pour une faïence on doit compter 10 à 15 points (x 10-7 °C-1) d'écart entre les valeurs de la pâte et de la glaçure, et pour un grès ou une porcelaine entre 1 et 5 points pour éviter le tressaillage.

 

Exemple :

- Pour une pâte de faïence ayant un coefficient de 80 x 10-7 °C-1, une glaçure ayant un coefficient de 65 à 70 x 10-7 °C-1 est souhaitable.

- Pour une pâte à porcelaine ayant un coefficient de 53 x 10-7 °C-1, une glaçure comprise entre 48 et 51 x 10-7 pourra convenir.

 

Lors du refroidissement, les produits émaillés vont se rétracter et la glaçure sera mise en compression par le tesson dès quelle sera assez rigide (Les glaçures de faïence deviennent rigides généralement en dessous de 600°C). On procède ainsi parce que les glaçures résistent plus à l'effort de compression qu'à celui de traction. En comprimant la glaçure on s'éloigne donc du tressaillage (Le tressaillage est dû à une contrainte de traction trop élevée appliquée à la glaçure).

 

Généralement on met plus fortement en compression les glaçures de faïence pour anticiper le gonflement de la pâte lors du vieillissement. Les tessons poreux présentent souvent des phénomènes de réhydratation des silicates alcalins (Hydroxylation) qui les composent, ce qui se traduit par un gonflement du matériau produisant un effort de traction sur la glaçure. Cette réhydratation est souvent longue, cela peut mettre des années… ou être assez rapide sous l'effet d'une l'utilisation intensive (Pendre en compte l'utilisation du lave-vaisselle (*1) et du four à micro-ondes (*2)…). Si la compression de la glaçure est supérieure à la valeur du gonflement on évitera ainsi le tressaillage.

C'est différent pour un grès ou une porcelaine. Le tesson étant étanche ou très peu poreux, le gonflement sera inexistant. Les valeurs de dilatation de la pâte et de la glaçure pourront donc être assez proches.

 

(*1) Lave-vaisselle :

 

Le lave-vaisselle est un appareil domestique devenu courant. Ses fabricants argumentent l'économie d'énergie, d'eau, de bruit... c'est un des appareils ménagers le plus utilisé, il lave tout ensemble : verres, assiettes, couverts, tasses, plats, etc... faits de matières différentes : verre, cristal, porcelaine, grès, faïence, plastique, inox, acier émaillé, surfaces revétues en teflon, etc... et avec une seule lessive à la fois, c'est un vrai miracle dans une cuisine moderne. Pourtant cet appareil est un véritable outil de torture pour nos beaux ustensiles de table.

C'est l'effet de choc thermique lors du rinçage qui est le plus à craindre sur les produits émaillés. Certains lave-vaisselle chauffent jusqu'à 70°C et plus pendant la phase de nettoyage. Les contraintes de dilatations ne sont pas négligeables à cette température et les chocs thermiques lors des rinçages augmentent la fatigue des matériaux dont principalement celle de la glaçure. L'accélération du vieillissement des produits émaillés est une des conséquences de l'utilisation du lave-vaisselle (les autres conséquences néfastes étant le frottement mécanique et l'agression chimique par les produits lessiviels).

 

 

 

(*2) Four à micro-ondes :

 

Un four à micro-ondes est une enceinte dans laquelle sont dispersées des ondes électromagnétiques générées par un magnétron. Ces ondes ont une fréquence élevée : 2450 MHz (soit 49000 fois plus que le courant alternatif domestique dont la fréquence est de 50 Hz). Ces fortes oscillations du champ électromagnétique à raison de 2 millions et demi de fois par seconde sont particulièrement actives sur les molécules d'eau. Les molécule d'eau agitées en tous sens à cette fréquence élevée entrent en collision les unes avec les autres, ce qui produit de la chaleur et une élévation rapide de la température.

Les aliments (Viande, légumes, liquides…) contiennent de l'eau et sont échauffés facilement sous l'effet des micro-ondes. Les matériaux non métalliques ne s'échauffent pas sous l'effet des micro-ondes, c'est le cas des céramiques (Les métaux réfléchissent les micro-ondes).

Une céramique mise dans un four à micro-ondes ne chauffe pas. Elle se réchauffe seulement par le contact avec les aliments ou les liquides qu'elle contient.

Si cette céramique est poreuse et qu'elle a absorbé de l'eau lors de son utilisation (Lavage, trempage, fissures…) elle va s'échauffer " de l'intérieur " sous l'effet de l'agitation des molécules d'eau contenues dans ses pores. Ce type d'échauffement est particulièrement destructeur car il fait se dilater rapidement le tesson et reste sans action sur la glaçure. Le four à micro-ondes est un appareil qui fait vieillir prématurément les céramique poreuses en les conduisant irrémédiablement au tressaillage. Il faut éviter de mettre les faïences au four à micro-ondes, leur action fatigue mécaniquement les glaçures qui finissent à plus ou moins brève échéance par se fissurer. Ce n'est pas un défaut, mais une attention et un soin nécessaire à porter à ce matériau céramique pour qu'il garde ses plus beaux effets le plus longtemps possible, un peu comme on le fait pour l'entretien d'une lingerie en soie qui ne supporte qu'un lavage à l'eau tiède ou celui d'un cristal fin qu'on ne lave qu'à la main.

 

 

Calcul du coefficient de dilatation thermique d'une glaçure :

 

Plusieurs auteurs ont cherché à mettre en équation certaines propriétés du verre. Parmi eux A. A. Appen est celui qui a créé des outils donnant des résultats calculés au plus près des valeurs expérimentales. Contrairement à la plupart des autres auteurs, il fait intervenir ses calculs sur les fractions molaires des oxydes. Cette prise en compte de la dimension atomique des éléments est plus réaliste que les méthodes simplement basées sur le pourcentage pondéral.

Ces calculs destinés à déterminer les propriétés des verres sont applicables aux glaçures vitrifiées. Ils permettent d'orienter le céramiste en lui donnant la tendance des propriétés de d'une glaçure lorsqu'il en modifie la composition. Ce sont des valeurs relatives. Dans certains domaines de glaçures elles sont très proches des valeurs réelles.

 

Voici par valeur décroissante l'action des oxydes sur le coefficient de dilatation thermique selon A. A. Appen dans le domaine de 20 à 400°C (exprimée pour un calcul basé sur la fraction molaire de chaque constituant) :

 

 

Dans les explications suivantes " % " signifie fraction molaire

 

Calcul des variables pour le Plomb :

 

Si 0 £ S %R2O < 3 ,

ou Si ( S %RO + S %RmOn) / S %R2O > 0,333

prendre a PbO = 130 x 10-7 °C-1

Dans les autres cas a PbO = (130 + 5 ( S %R2O - 3)) x 10-7 °C-1

 

Calcul des variables pour le Titane :

 

a TiO2 = (30 - 1,5 ( %SiO2 - 50)) x 10-7 °C-1 pour 80 ³ %SiO2 ³ 50

a TiO2 = 30 x 10-7 °C-1 pour %SiO2 < 50

 

Calcul des variables pour la Silice :

 

a SiO2 = (38 - (%SiO2 - 67)) x 10-7 °C-1 pour 100 ³ %SiO2 ³ 67

a SiO2 = 38 x 10-7 °C-1 pour %SiO2 £ 67

 

Calcul des variables pour le Bore :

 

y = [ S %R2O + S %RO - 2%BeO - e ( %Al2O3 - %PbO - %ZnO)] / %B2O3

avec e = 0 si (%Al2O3 - %PbO - %ZnO) < 0, sinon e = 1

 

Si y > 4, a B2O3 = - 50 x 10-7 °C-1

Si y < 4, a B2O3 = 12,5 ( 4 - y ) - 50 x 10-7 °C-1

 

 

 

II ) La Couche Intermédiaire :

 

Les coefficients de dilatation de la pâte ou de la glaçure sont mesurés séparément. On mesure la dilatation d'un barreau de pâte ou d'un barreau de glaçure à l'aide du dilatomètre, mais rien ne laisse présager avec certitude ce qu'il va advenir de l'union de ces deux matériaux sous l'effet de la cuisson.

 

La glaçure par sa nature et son état de fusion avancé lors de la cuisson va se comporter comme un solvant et dissoudre la pâte partiellement. Le niveau d'altération du tesson par la glaçure va dépendre de l'agressivité de la glaçure et de ses fondants, de la composition du tesson et de sa finesse, de la température et de la durée de la phase active de la glaçure fondue.

Il en résultera une couche " mêlée " graduelle issue de l'action dissolvante de la glaçure sur le tesson. La progressivité des propriétés de composition de la glaçure vers celles du tesson dans cette couche intermédiaire crée l'intimité nécessaire aux deux matériaux pour produire une union durable. Plus cette couche sera importante et plus les tensions de la pâte sur la glaçure seront amorties.

 

Il arrive que certaines glaçures non conformes d'un point de vue dilatométrique et qui devraient produire du tressaillage sur un tesson donné ne le fassent pas. C'est ce qui arrive lorsqu'une glaçure forme une couche intermédiaire qui dissout fortement un tesson siliceux. L'enrichissement de la couche de glaçure en silice abaisse sa dilatation jusqu'au point de former un accord convenable avec le tesson.

Pour les mêmes raisons, le tressaillage peut également disparaître lorsqu'on recuit une pièce déjà trésaillée. La seconde cuisson enrichissant la glaçure en silice par l'action de sa couche intermédiaire, les tensions internes passent sous la limite de rupture. Ce phénomène est couramment constaté pour les faïences.

 

Écaillage : Lorsque la couche intermédiaire est absente ou insuffisante, l'écaillage se produit la plupart du temps. C'est le cas lorsque le biscuit présente une surface farineuse due à des poussières minérales avant émaillage, ou encore lorsque les parties grattées ou poncées présentent une surface peu compacte avec des particules se détachant facilement. Pendant la cuisson, la glaçure va fondre et " digérer " en partie les ingrédients de surface mal fixés et écailler au refroidissement lorsque les tensions de compression se produiront. La glaçure ne peut supporter une mise en compression sans se rompre que si elle est solidement " soudée " au tesson par la couche intermédiaire.

 

 

 

III ) L'Elasticité de la glaçure :

 

Comme je l'ai indiqué dans le paragraphe sur la dilatation, l'ordre de grandeur de l'allongement d'un produit céramique sous l'effet de la chaleur est très faible, il est de quelques microns par mètre et par degré de température.

Une glaçure dont la couche est très fine comparée à celle du tesson est donc très facilement dommageable. C'est elle qui subit directement le chaud ou le froid en surface du produit céramique lors de son utilisation. La glaçure est donc exposée très souvent à des chocs thermiques et sollicitée en alternance par des contraintes de compression et de traction. Ce sont ces contraintes en accordéon qui " fatiguent " les glaçures insuffisamment accordées sur un tesson.

 

La notion d'élasticité prend toute son importance dans la longévité de l'accord glaçure/tesson. Sans une certaine rigidité de la glaçure, celle-ci serait rapidement rompue.

 

L'élasticité dépend de la composition de la glaçure, selon les oxydes présents et leurs proportions. Elle est également affectée par l'action de la couche intermédiaire si celle-ci est importante.

 

 

Rappels sur l'élasticité :

 

Un corps solide qui se déforme sous l'action d'une contrainte et reprend sa forme lorsque cesse cette contrainte est dit " élastique " ou " fragile " (Selon la Loi de Hooke, la déformation est proportionnelle à la contrainte appliquée pour un corps élastique. La constante de proportionnalité est appelée " module ").

Sous une contrainte de traction, apparaît un allongement caractérisé par le module d'élasticité " E " (module d'allongement ou module de Young).

 

 

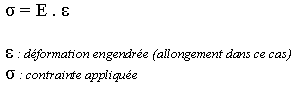s : en Newton par cm² (F / S)

e : sans unité (L-Lo / Lo)

L'unité pour le module E est donc le N/cm² ou le Gpa.

 

Ce module sera d'autant plus élevé que la déformation sera faible pour une contrainte élevée, c'est ce que l'on doit rechercher à propos des glaçures céramiques.

 

Plus le module de Young est élevé plus la glaçure est "rigide"

 

Le comportement à la fatigue de la glaçure résulte de son allongement sous l'effet des contraintes dues aux variations de température. La durée de vie de la glaçure est de ce fait directement liée à son module d'élasticité (E ou module de Young). Plus ce module sera élevé, moins la glaçure se déformera sous l'effet des variations de température et plus sa durée de vie sera importante. Ceci à la condition que la contrainte appliquée ne dépasse pas la limite mécanique supportable par la glaçure. Sinon c'est la rupture.

 

 

 

tressaillage, dilatation, dilatomètre, analyse, mesure, instruments de mesure, dilatation thermique, dilatométrie, four, chaleur, élasticité, module de young, résistance mécanique

 

 

 

 

Calcul du module d'allongement (ou module de Young) d'une glaçure :

 

Plusieurs auteurs ont cherché à mettre en équation certaines propriétés du verre. Parmi eux A. A. Appen est celui qui a créé des outils donnant des résultats calculés au plus près des valeurs expérimentales. Contrairement à la plupart des autres auteurs, il fait intervenir ses calculs sur les fractions molaires des oxydes. Cette prise en compte de la dimension atomique des éléments est plus réaliste que les méthodes simplement basées sur le pourcentage pondéral.

Ces calculs destinés à déterminer les propriétés des verres sont applicables aux glaçures vitrifiées. Ils permettent d'orienter le céramiste en lui donnant la tendance des propriétés de d'une glaçure lorsqu'il en modifie la composition. Ce sont des valeurs relatives. Dans certains domaines de glaçures elles sont très proches des valeurs réelles.

 

Voici par valeur décroissante l'action des oxydes sur le module de Young ( E ) selon A. A. Appen (exprimée pour un calcul basé sur la fraction molaire de chaque constituant) :

 

 

Oxyde	E en kgf/cm²	E en N/cm²	E en KBar
ZrO2	18.70 x 105	183.44 x 105	1833.8
B2O3 (selon composition)	1.00 à 18.00 x 105	9.81 à 176.58 x 105	98.0 à 1765.2
TiO2	17.10 x 105	167.75 x 105	1676.9
La2O3	14.00 x 105	137.34 x 105	1372.9
MnO	12.88 x 105	126.35 x 105	1263.1
Al2O3	11.40 x 105	111.83 x 105	1117.9
CaO	11.15 x 105	109.38 x 105	1093.4
BeO	10.90 x 105	106.93 x 105	1068.9
SrO	9.62 x 105	94.37 x 105	943.4
MgO	9.20 x 105	90.25 x 105	902.2
CoO	8.52 x 105	83.58 x 105	835.5
Li2O	8.00 x 105	78.48 x 105	784.5
SiO2 (selon composition)	6.50 à 7.10 x 105	63.76 à 69.65 x 105	637.4 à 696.3
BaO	6.25 x 105	61.31 x 105	612.9
NiO	6.12 x 105	60.04 x 105	600.1
ZnO	6.00 x 105	58.86 x 105	588.4
Na2O	5.95 x 105	58.37 x 105	583.5
CdO	5.70 x 105	55.92 x 105	559.0
Fe2O3	5.21 x 105	51.11 x 105	510.9
P2O5	5.20 x 105	51.01 x 105	509.9
PbO	4.30 x 105	42.18 x 105	421.7
K2O	4.10 x 105	40.22 x 105	402.1

 

Dans les explications suivantes " % " signifie fraction molaire

 

Calcul des variables pour le Bore :

 

y = [S %R2O + S %RO + %Al2O3] / %B2O3

 

Si y > 2 , E _B2O3 = 18.00 * 10⁵ kgf/cm²

Si 2 ³ y ³ 1, E _B2O3 = (12.00 + 3 y ) * 10⁵ kgf/cm²

Si 1 ³ y ³ 0, E _B2O3 = (1.00 + 14 y ) * 10⁵ kgf/cm²

 

Multiplier le résultat par 9.81 pour obtenir E en N/cm², et par 0.980665 pour obtenir E en Kbar

 

Calcul des variables pour la Silice :

 

Si 100 ³ %SiO2 ³ 67, E _SiO2 = (5.30 + 0.018 %SiO2) * 10⁵ kgf/cm²

Si %SiO2 £ 67, E _SiO2 = 6.50 * 10⁵ kgf/cm²

 

Multiplier le résultat par 9.81 pour obtenir E en N/cm², et par 0.980665 pour obtenir E en Kbar

 

 

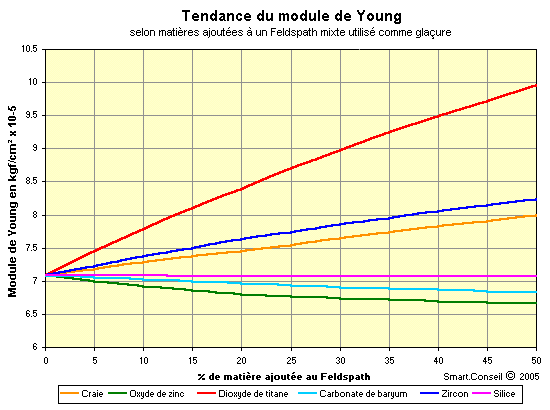
Exemple de tendances sur le module Young pour des ajouts de 0 à 50 % de différents oxydes sur une glaçure formée à partir d'un feldspath mixte :

 

La composition du feldspath est la suivante (En % pondéral) :

 

RO - R2O	Amphotères	RO2
CaO ----- 0.42	Al2O3 -----17.28	SiO2 ----- 69.70
MgO ----- 0.06	Fe2O3 ----- 0.19	TiO2 ----- 0.10
BaO ----- 0.18	-----	-----
Na2O ----- 4.02	-----	autres
K2O ----- 8.01	-----	P2O5 ----- 0.05

 

 

 

 

 

On voit très bien la tendance qu'offre l'ajout de craie et/ou de titane dans cette glaçure pour renforcer son module d'allongement.

 

 

 

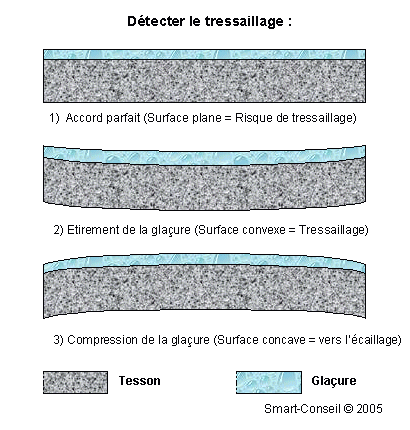
IV ) Méthode simple pour savoir si une glaçure va tressailler :

 

Il suffit d'émailler sur une seule face des petites plaquettes biscuitées bien planes de la terre à tester avec la glaçure. Dimension recommandées : 100 x 100 x 5 mm. Cuire ces plaquettes et observer leur profil :

 

 

 

 

 

tressaillage, dilatation, dilatomètre, analyse, mesure, instruments de mesure, dilatation thermique, dilatométrie, four, chaleur, coefficient de dilatation, rupture élastique

 

 

 

 

 

V ) Logiciel de calcul du coefficient de dilatation thermique et du module de Young sur tableau Excel à télécharger :

 

Voici une feuille de calcul sous Excel à télécharger. Elle contient la procédure de calcul du coefficient de dilatation et du module de Young selon la méthode de A. A. Appen pour les oxydes les plus courants en glaçures céramiques (sauf les oxydes colorants).

Les données par défaut qui figurent déjà dans les cases jaunes d'entrée correspondent à la formule de la fritte Ferro 3110, pour exemple :

 

 

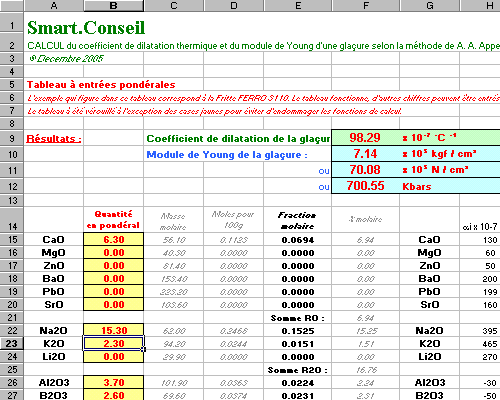 Extrait de la fenêtre de calcul sous Excel

 

Le tableau fonctionne. Les données d'entrée sont en valeurs pondérales. Il faut les inscrire dans les cases jaunes prévues à cet effet.

Le tableau est protégé en écriture à l'exception des cases jaunes pour éviter la destruction des formules de calcul par erreur.

La conversion des valeurs pondérales est faite en fractions molaires, en % molaires et en formule de Seger.

Pour vous exercer vous pourrez facilement reproduire le graphique de tendance du module de Young selon l'ajout de matières au feldspath mixte pour l'oxyde de zinc (ZnO), la silice (SiO2) et le dioxyde de titane (TiO2).

 

Ce fichier a été soumis à un antivirus avant mise en ligne, il est sous forme d'archive au format ZIP.

 

 

Téléchargement / downloading 

 

 

 

Smart2000.fr © Décembre 2005 - FRANCE

Écrit et documenté par le propriétaire du site // Contact : Smart2000@wanadoo.fr

Document pour CONSULTATION PRIVÉE uniquement

Toute reproduction totale ou partielle est interdite

 

 

---

 

Smart2000.fr le site dédié aux passionnés de céramique

 

Smart2000 - FRANCE sur https://smart2000.fr/

 

This entire page Copyright © JUIN 2005-2023, All Rights Reserved.

Les textes et les photos restent la propriété de leur auteurs, ils ne peuvent être réutilisés sans un accord préalable. Nous consulter.